What this is: I am going to highlight problems I used with my honors geometry students that I thought were valuable. You can see all posts in this series here. I am taking no claim that these are necessarily original as I might have stolen them from many of you reading this!
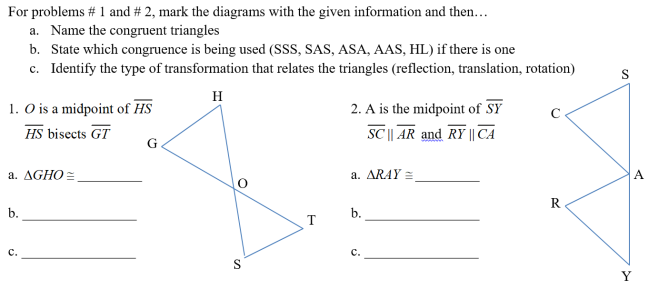
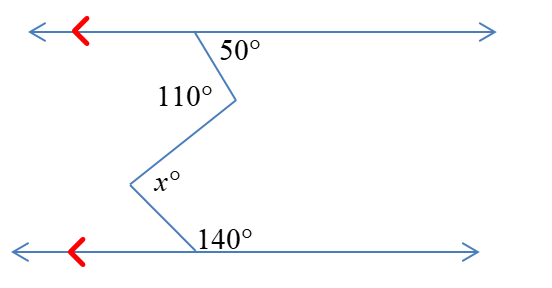
How I used it: This was a review problem I gave in class.
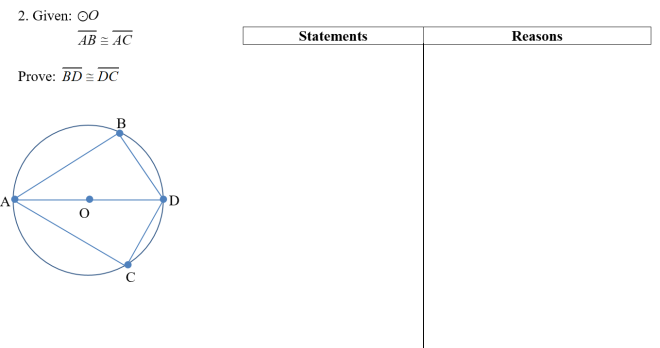
What is it: This was a problem to practice and review proof skills.
Why I like it: This involves a few different ideas such as auxiliary segments and you can prove a couple different pairs of triangles. Their is also a couple different ways (as well as ways that would not work) so it was a great exercise for the learners to determine how much proof practice they needed. It made my top kids stop and think for a moment so that is always a good thing!
Let me know if you used this and how it went!